Areas on the Cross-Section Diagram 解き方メモ

模式断面図の面積 | アルゴリズムとデータ構造 | Aizu Online Judgeを解く時に苦労したのでそのメモφ(･･

問題

模式断面図の面積 | アルゴリズムとデータ構造 | Aizu Online Judgeに書いてある通りです、ってのも素っ気ないので以下にスクショ貼ります。

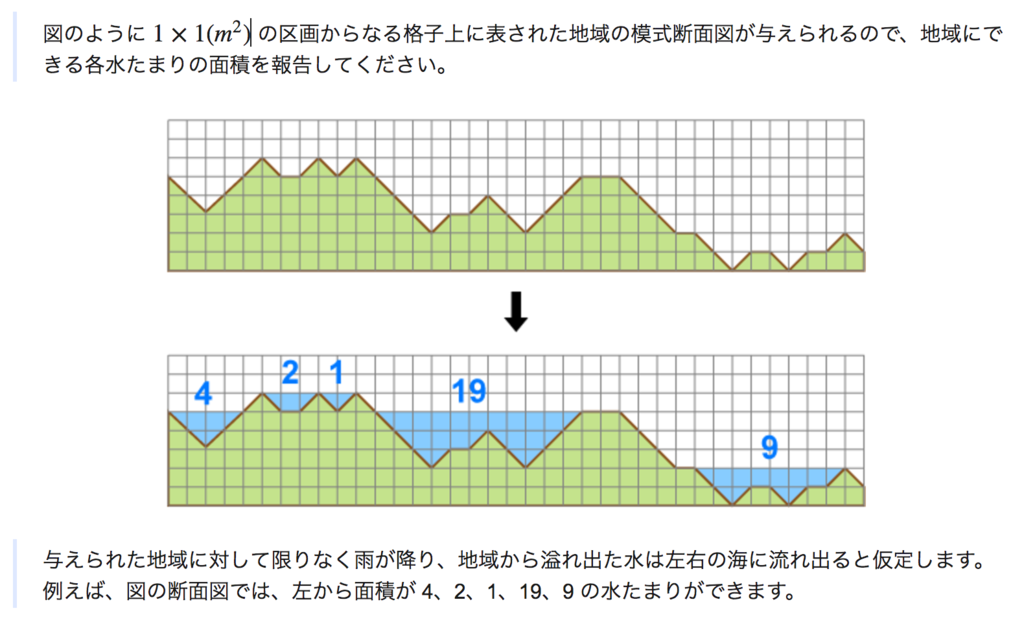
図のような状況において、水たまりそれぞれの面積と全体の面積を出すという問題です。

入力として\、_、/の列を受け取り、出力は全総面積、水たまりの数、各水たまりの面積になります。

上の図に対応する入力、出力は以下のようになります。 出力は総面積が35、水たまりの数が5、各水たまりの面積が4 2 1 19 9となっていることを示しています。

考え方

最初自力で考えてたんですが、全くわからなかったのでALDS1_3_D: Areas on the Cross-Section Diagram - State-of-the-Arsのコードを参考にしながら考えていきました。

コードを読んで参考になった考え方は、

• \の場所をスタックに保存することで、/を受け取った時にそれと対応する\を見つけることができる
• 上記の方法で、対応する\、/を用いて面積を計算すること = 横向きに面積を計算していくということ

アルゴリズムとしては、

• 入力が\のときはそのインデックスをスタックに保存する
• 入力が/の時はスタックからpopし、現在のインデックスと組み合わせて横向きに面積を計算する
• 計算した面積の総和をとって総面積を計算する

といった感じです。

ただ、これだけでは各水たまりの面積を計算できないので、

• /の時にpopしたインデックスと計算した面積のタプルを保存する
• 必要に応じて上記のタプルを結合していく(水たまりを結合する操作に相当)

ということもします。

以上のために2つのスタックを用意します。

1. \のインデックスを保存するスタック
2. popしたインデックスと計算した面積のタプルを保存するスタック

これだけだと意味不明なので例を出しながら説明します。

具体例で説明

具体例として、先ほどの問題の水たまりが1, 19となっている箇所を用いて説明します。

ちなみに入力は\/\\\\/_/\\///となります。 今後はこの入力をインデックスと合わせて説明するので、簡単な表を書いておきます。

index	0	1	2	3	4	5	6	7	8	9	10	11	12	13
value	\	/	\	\	\	\	/	_	/	\	\	/	/	/

index = 0

\なのでスタック1にインデックスを保存します。

stack	stack2
0

index = 1

/なのでスタック1からpopします。

面積 = (現在のindex) - (popしたindex) = 1 - 0 = 1となります。 popしたインデックスとこの計算結果をスタック2に保存します。

stack	stack2
	(0, 1)

index = 2 ~ 5

\らをスタック1に積んでいきます。

stack	stack2
5
4
3
2	(0, 1)

index = 6

/なのでスタック1からpopします。

面積 = 6 - 5 = 1となります。

popしたindexの5は、スタック2に保存したタプルに入っているindexである0より大きいので、そのままスタック2に保存します。

stack	stack2
4
3	(5, 1)
2	(0, 1)

スタック2が水たまりの様子を表しているので、これは面積1の水たまりが2つあることを示しています。 実際にここまで読み込んだ時の様子は以下のようになっています。

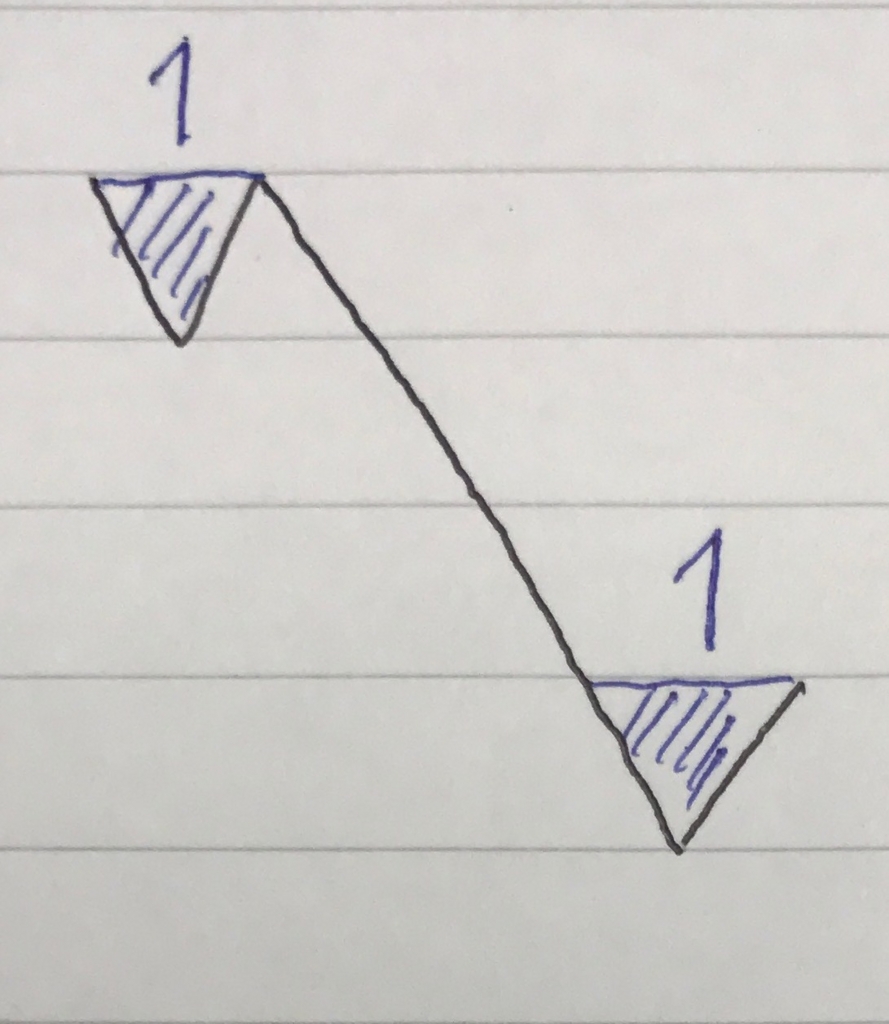
index = 7, 8

index = 7のとき_なので特に何もしません。 index = 8のとき/なので、スタック1からpopします。

面積 = 8 - 4 = 4となります。

popしたindexである4はスタック2に積まれているタプルに保存されたindexである5より小さいので、水たまりは結合されます。 したがって、popしたindexである4と面積 = (タプルに保存されていた面積である) + (先ほど計算した面積) = 1 + 4 = 5を合わせて保存します。 この時のスタックの状態は以下のようになります。

stack	stack2
3	(4, 5)
2	(0, 1)

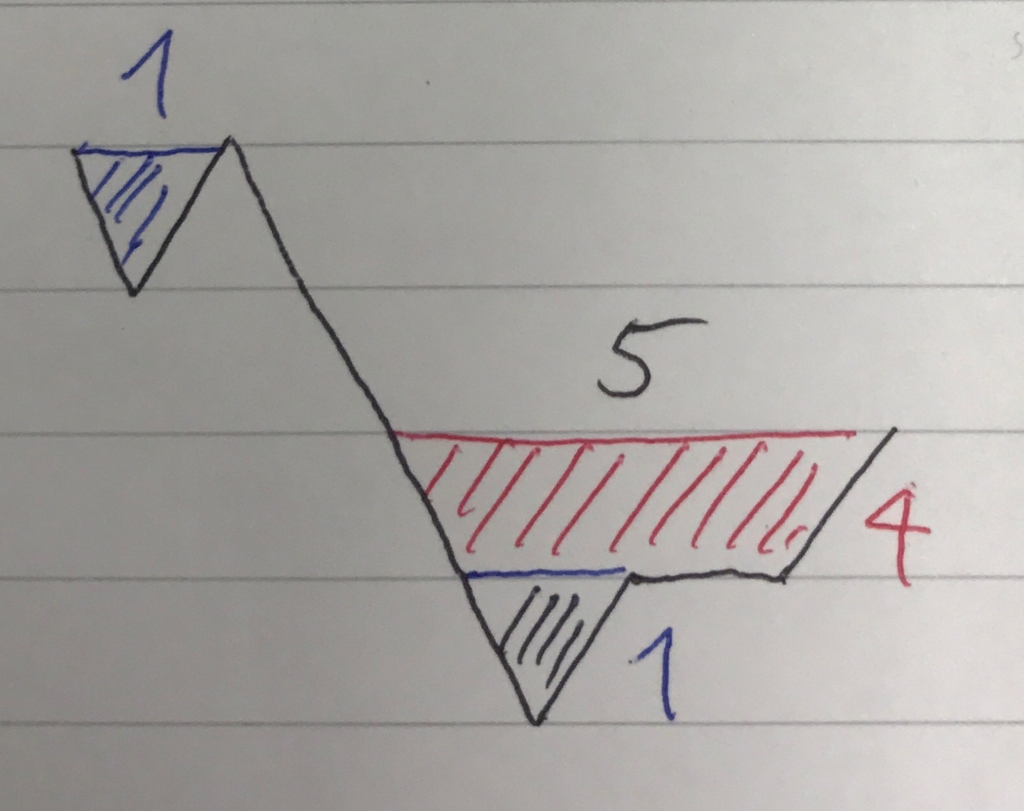
index = 9, 10

ちょっと面倒になってきたのでスタックの状態だけ、、

stack	stack2
10
9
3	(4, 5)
2	(0, 1)

index = 11

stack	stack2
9	(10, 1)
3	(4, 5)
2	(0, 1)

index = 12

stack	stack2
	(9, 4)
3	(4, 5)
2	(0, 1)

この時の状態はこんな感じ。

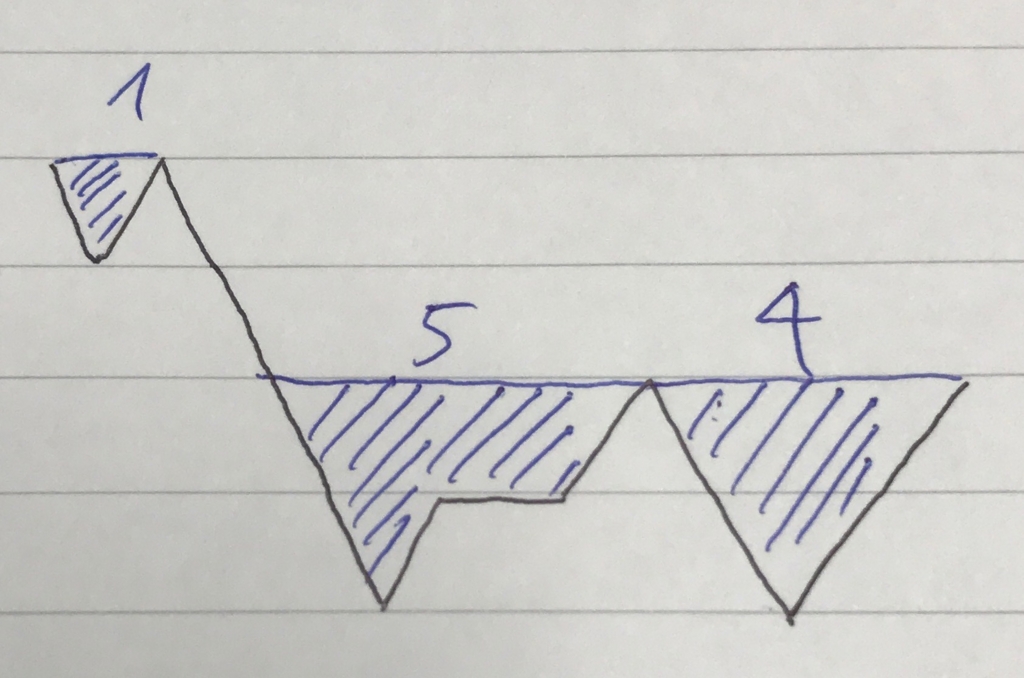
index = 13

/なのでスタック1から3をpopする。

面積 = 13 - 3 = 10となる。

popしたindexである3に対して、スタック2にある(4, 5), (9, 4)はindexの値が大きいのでこれらを結合する。

stack	stack2
	(3, 19)
2	(0, 1)

図的にはこんな感じ。

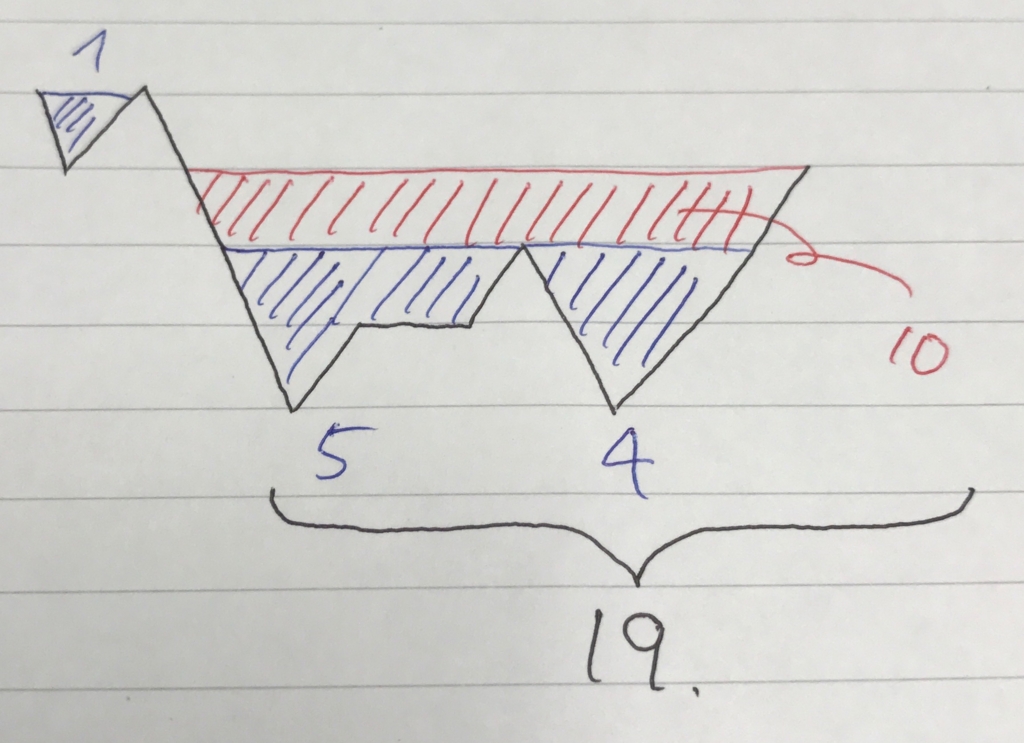
結果

スタックの状態は以下のとおり。

したがって、スタック2を見ると、面積1の水たまりと、面積19の水たまりがあることがわかる。

stack	stack2
	(3, 19)
2	(0, 1)

コード

rubyで書きました。

コードは以下の通り。まだ最適化できそうやけどとりあえずはこれで解けます。

sum = 0
stack = [] # \を受け取ったindexのstack
res = [] # /に対応する\のindexとその時に計算した面積のtupleのstack. 最後に各断面の面積として表示する
gets.split("").each_with_index { |v, i|
  if v == "\\"
    stack << i
  elsif v == "/"
    j = stack.pop
    if !j.nil? # \より先に/が来たときのため
      a = i - j # indexの引き算で横向きに計算する
      sum += a

      loop do
        k, b = res.pop
        if !k.nil?
          if j < k
            a += b
          else
            res << [k, b] # 一旦popしてるので特に何もなければ再度pushして戻す
            break
          end
        else
          break
        end
      end
      res << [j, a]
    end
  end
}
puts sum
if res.size() == 0
  puts "0"
else
  puts "#{res.size()} #{res.map{|n| n[1]}.join(" ")}" # size == 0の時にmapがうまくいかない??
end

githubにもあげてます。

github.com

最後に

今回は最初さっぱりわからず30分くらい問題とにらめっこしてたのですが、横向きに面積を計算する、その時面積はインデックスの引き算で求めることができる、ということに気づくと後はすぐに解けました。

見方を変えれば簡単に解けるけど、その見方に気付けないという典型的な問題でした。

こういう見方は普段から引き出しを増やすしかないのかなーと思うので今後も勉強を続けていきたいなーと思いました。